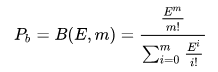Erlang's work on telephone systems in the early 20th century is foundational to how we think about, and build, distributed and cloud systems 100 years later. How can this work, done before modern computing was even a field, be so important?

Erlang spent a big part of his career thinking about how to apply statistics to the behavior of telephone networks. Given a certain amount of capacity, how many customers can this telephone system serve? As our customer base grows, how will the quality of service they get change?

In 1909, Erlang proved that (given some reasonable assumptions) that the number of calls arriving during a given time interval follows the Poisson distribution. Today, we still use Poisson processes to model the arrival rate of clients in cloud systems: en.wikipedia.org/wiki/Poisson_d…

In 1917, Erlang published what is now know as the Erlang loss formula (or Erlang-B). Given a telephone network with m lines, and an offered load of E erlangs, what is the probability that a call will have to be rejected because no line is available?

This is still a very relevant question, because cloud systems need the same answer. Given an arriving load, and some number of servers (or threads, or connections) available, what is the probability we will need to reject a customer?

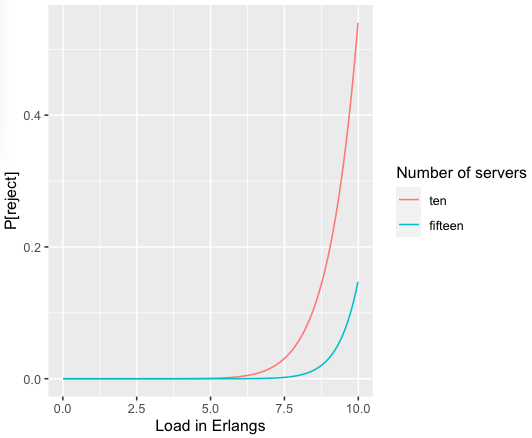
For example, we can apply Erlang's B formula to estimate the probability that a fleet of 10 or 15 servers would reject a customer's request (assuming one request per server at a time):

Did increasing the fleet size by 50% have as big an effect as you would have assumed?

I've kept calling this unit of load Erlangs, what's up with that? The offered traffic is simply the mean arrival rate multiplied by the mean call holding time. So if you're getting 100 calls a second, and each takes 1ms, your load is 0.1 Erlangs. It was named for Erlang in 1946.

Does load = arrival rate * processing time remind you of Little's Law? If not, it should: en.wikipedia.org/wiki/Little%27… Little's law directly connects load and concurrency.

This is just scratching the surface of Erlang's work on telephone systems. It's amazing how far Erlang (and others) got in the early decades of the 20th century, and how applicable that work still is to systems far beyond what they could have imagined in sophistication and scale.