I decided to share an idea that I haven’t been able to work on for quite some time so that others may enjoy (and hopefully help me out.) A recreational mathematics thread: The transfinite Rubik’s cube.

I learned how to solve a Rubik’s cube only few years ago. While I never turned it into an obsession and stayed only as a beginner, as a subscriber of the Cantorian religion of mathematics, I thought about how an infinite Rubik’s cube should look like.

I have found some proposals on the web but I don’t think they are the correct generalization. Here I introduce: The transfinite Rubik’s cube. To be fair, it is likely that someone else also came up with the same natural generalization so I am reluctant to claim originality.

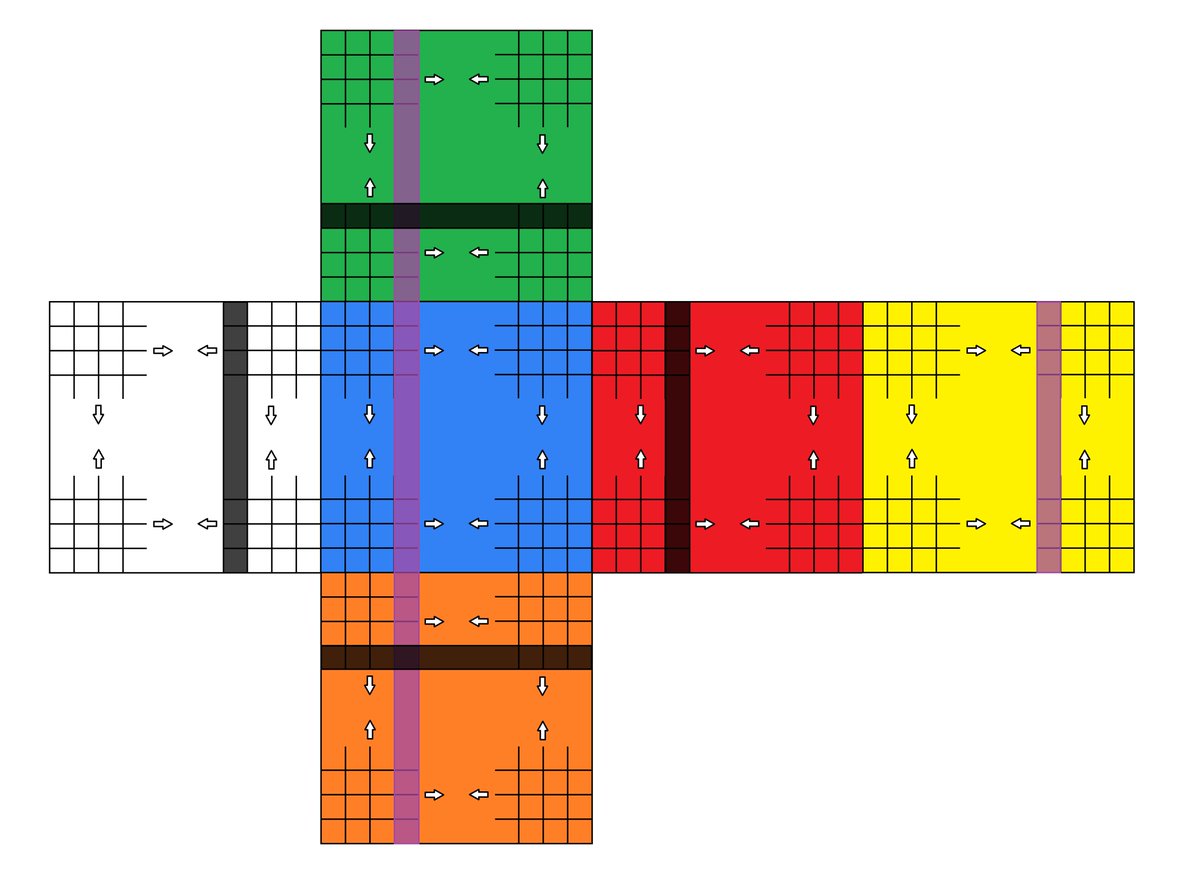
The transfinite Rubik’s cube (of type ω+ω*) is a cube that is supposed to be the "limit" of n⨯n⨯n Rubik’s cubes as you align the corner cubes, their adjacent cubes etc. Below is an illustration of how the transfinite Rubik's cube would look once it is unfolded.

Formally, we can define the transfinite Rubik's cube to be the cartesian product R=(ω+ω*)⨯(ω+ω*)⨯{1,2,3,4,5,6} where ω={0,1,2,...} and ω*={0*,1*,2*,...}. Here the element (i,j,k) represents the facet on the k-th face with coordinates (i,j).

The transfinite Rubik's cube has countably infinitely many rotations. The usual cube rotations can be formally defined by setting up three maps α(n),β(n),γ(n) : R→R for each n∈ω+ω*. These maps rotate the n-th layer on each axes according to some fixed enumeration of layers.

For example, suppose that α(3) rotates the purple layer “downwards” and β(3) rotates the black layer “clockwise”. Then α(3)(i,j,green)=(i,j,blue) α(3)(i,j,orange)=(i*,j*,yellow) β(3)(i,j,white)=(j,i*,green) where n**=n. (Of course I should have really used the codes of colors.)

Since we have infinitely many possible moves in the transfinite cube, it is natural (and indeed, expected) to allow infinitely many moves to be played provided that there is a "limit" cube.

More formally, we shall call a sequence ζ=(ζₙ(iₙ)) of rotations valid if every facet eventually stabilizes under the action of ζ, that is, the sequence ζ(x)=(ζₙ(iₙ)(x)) of elements of R is eventually constant where ζₙ is one of α,β,γ and iₙ is in ω+ω*.

At this point, you should realize that mathematical details don't matter much. The point is that we can construct a transfinite Rubik's cube model with properly defined rotations. From now on, you can ignore the formalization, just use your imagination.

Here is a seemingly basic question: Suppose that you scramble the cube by an infinite valid sequence of moves that provides you a "limit" cube. Is it possible to unscramble the cube? Your first reaction may be "of course, just apply the opposite moves." But hold on...

Assume that the valid sequence of moves you applied is (ζ₀(i₀),ζ₁(i₁),…). Then the inverse is supposed to be "the sequence of moves (…,ζ₁(i₁),ζ₀(i₀))" but there is no such thing since our sequences of moves are supposed to be indexed by ordinals, preferably ω.

Given a valid sequence (ζ₀(i₀),ζ₁(i₁),…), can we always find a sequence of moves that will act as the inverse of this sequence? I do not know the answer.

I thought that this may be proven in a general framework that forgets the details of Rubik's cube setting and abstracts the ideas here, so I asked the following MO question some time ago: mathoverflow.net/questions/3523… However, I have not made any progress.

You may be wondering how an infinite valid sequence of moves would transform the cube. Before I gave a concrete example, let us make the following simple but important observation: If ζ(n)(i,j,k)=(p,q,r), then {i,i*,j,j*}={p,q,p*,q*}.

That is, the orbit of a facet under a rotation is finite. It follows that any rotation can appear only finitely many times in a valid sequence of moves for otherwise there would be facets moving infinitely many times that prevents the cube from having a limit.

Now comes the concrete example. Suppose that we apply the valid sequence (α(0),β(0),α(1),β(1),α(2),β(2),…) of moves to the cube in the first image. After the cube stabilizes after ω many steps, we end up with the pattern in the second image. Can you unscramble it?

As I said, I am only a beginner so I asked an experienced cuber friend of mine how n⨯n⨯n cubes with n≥4 are solved. He told me that the general idea is to always reduce to the 3⨯3⨯3 case by solving "the center" first and treating the whole center as a single block piece.

The problem here is that it is not clear how to solve "the center" in the transfinite cube. Since "the center" for a color has infinitely many facets, each "solving the center" would require at least ω steps to group facets together, if there is any method at all.

Can we combine these solve the center moves into a single infinite sequence? I don't know. If not, the reduction to 3⨯3⨯3 strategy would require more than ω steps. My guess is that, if there is a method to unscramble every scrambled cube, it would require > ω but < ω² steps.

It is not clear to me whether every cube scrambled by a valid sequence of length ω can be unscrambled even if we use > ω steps. It would be mathematically interesting if this were not the case. What is your guess?

Please let me know if you spot any typos or conceptual errors. I'd be really glad if someone solved any of the questions that I asked above. Due to more "serious" obligations, I was not able to spend much time on such recreational matters.

I thought I should tag you here @Joel David Hamkins as I know that you are interested in transfinite generalizations of popular games.